Soft Matter

Soft Matter is an immense field of research that encompasses from polymers and colloids to liquid crystals, amphiphilic and surfactant systems, as well as biological systems. The following pentagon scheme shows some of the main areas of research inside this field
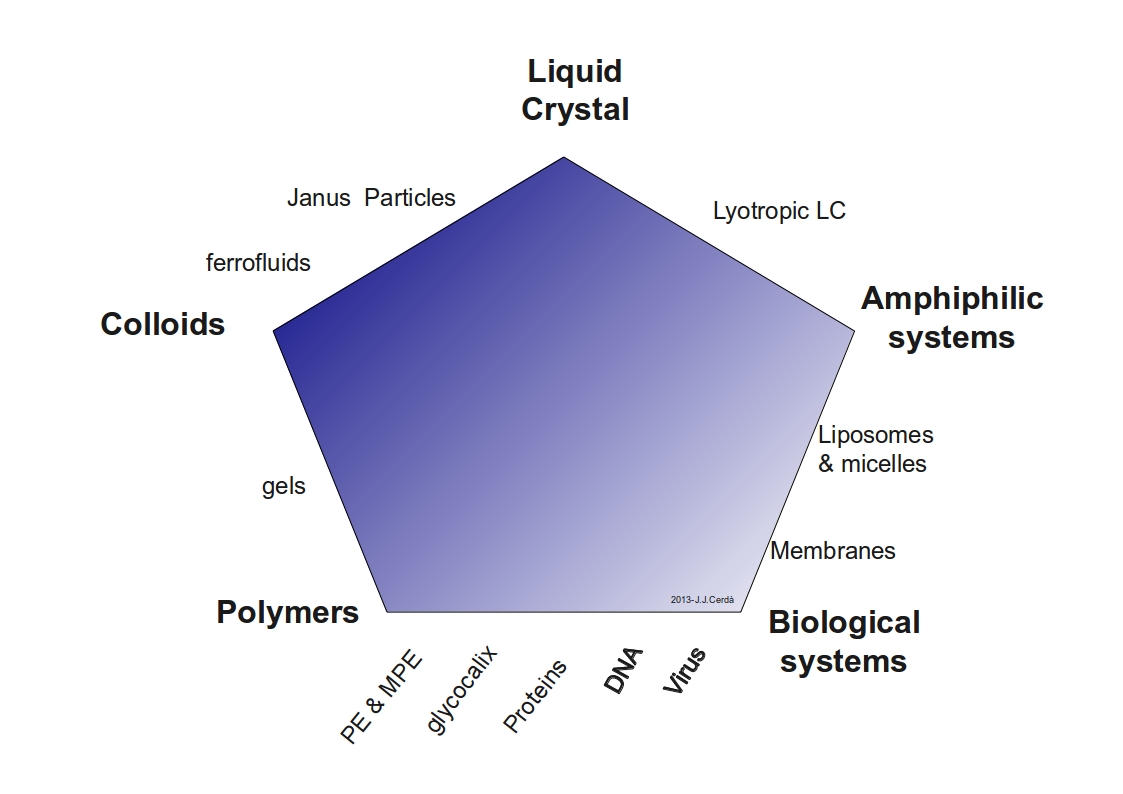
For a further insight onto the topic you can also check De Gennes Lecture on Soft Matter.
In the ONL group we do research in the following particular areas of Soft Matter, just click on the left menu to go directly to each one of the research fields in which we are doing research.
[1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53]
Glycocalyx
THE ENDOTHELIAL GLYCOCALYX AND ITS IMPORTANCE
Behind these two words lies an structure whose existence was confirmed in mammals just before humans landed on the moon. This system, in an adult human, weighs as much as the brain—approximately 1.4 kilograms—and if it were fully unfolded, it would easily cover more than three basketball courts. What differentiates it from other organs is that it is not located in any specific part of the body; on the contrary, it is found everywhere, in direct contact with the blood, resembling a soft velvet layer that internally covers all the arteries and veins of the body, from the largest ones to the smallest microcapillaries.
The thickness of this velvet covering we all have inside ranges between ten-thousandths and one-thousandth of a millimeter. But do not be deceived by its size: although it may seem like a minor thing not worthy of being considered a vital organ, the endothelial glycocalyx performs several critically important functions: it acts as a selective barrier, only allowing certain molecules to pass from the blood into the rest of the body, and protects us against fluid loss (edemas); it serves as a lubricating layer for transporting red blood cells, which is particularly important in the case of microcapillaries, where their openings can be smaller than the red blood cell itself; it prevents erosion of the walls of veins and arteries, and also greatly reduces the chances of other particles flowing through the blood adhering to the walls and causing clots and obstructions; furthermore, by capturing certain molecules, it controls the onset of thrombosis, inflammation, and oxidative stress. Another essential function of the glycocalyx, through the forces exerted by the blood upon it, is to send information to the cells forming the walls of the blood vessels (endothelium), so they modify their shape, size, and other properties, ensuring optimal blood flow in every moment and situation. Moreover, the glycocalyx also regulates the growth and migration of these endothelial cells throughout the body.
The vital role of the glycocalyx becomes evident when this covering disappears partially or totally: atherosclerosis quickly begins, and atheromatous plaques soon block the blood flow. Its loss has also been linked to strokes, hypertension, preeclampsia, and severe bacterial infections: some bacteria produce toxins that damage the glycocalyx as a strategy to penetrate every nook and cranny of the human body. Recent research in 2019 found that if the glycocalyx is damaged when a person contracts malaria, the chances of survival drop drastically. The glycocalyx also plays a major role in the growth and migration of tumor cells (metastasis) according to recent studies. Furthermore, strong evidence suggests that many of the complications that arise over time with diabetes (eye lesions that can lead to blindness, kidney damage, nerve damage, and small vessels that can lead to diabetic foot and gangrene) come from the fact that the disease significantly deteriorates the glycocalyx of the microcapillaries.
Thus, the glycocalyx has become an important therapeutic target in research aimed at curing or alleviating complications of certain diseases that afflict humanity. Despite the growing interest, the great challenge, fifty-five years after the discovery of the glycocalyx in mammals, is that, in many respects, the glycocalyx is still a great unknown. The initial neglect of its importance, its fragility, small size, and the difficulty of observing it in action in live studies have contributed to significant gaps in knowledge about its function, the mechanisms associated with its malfunction, and how these cause disruptions throughout the body. These gaps mean that medical advances are more the result of a slow learning process through trial and error than driven by a fundamental understanding of this complex organ. Undoubtedly, a better understanding of how the complex glycocalyx works would significantly accelerate medical advances.
If you want to see a video about the glycocalix we prepared for a scientific fair at the UIB university click on this link (only a version in Catalan of the video is available at this moment).
OUR RESEARCH
At the UIB, in our ONL research group, we have set out to
Contribute to improving the understanding of the glycocalyx and related diseases. Given the difficulty of studying and drawing conclusions from live studies, we have decided to address the problem using numerical simulations that model in great detail how the glycocalyx behaves when subjected to the flow of a fluid similar to blood. To achieve this detailed “in silico” model of the glycocalyx, the first task was to devise and build new algorithms that allow us to simulate such large and complex systems in a reasonable amount of time, with all the necessary detail to obtain reliable and quantitative results. This has been the first task completed in our GLYCOSIM project: we have developed the necessary computational tools, which will soon be available to other interested groups, and with these new tools, we are now investigating in detail two basic phenomena that are still poorly understood: how the glycocalyx modifies the properties of the fluids and red blood cells circulating inside microcapillaries, and the role of the glycocalyx in the initiation of obstructive deposits within microcapillaries. These are just the first steps towards fully understanding the glycocalyx, but they will undoubtedly bring us closer to the ultimate goal.
Through our “LEGOCITS” LEGOCITS project we aim to use what we have learned from the glycocalyx to answer several key questions, from both basic science and applied science, in orde to be able to design optimized artificial coatings.
The ONL group thanks the funding provided via the following Spanish national projects:


Ferrofluids
What are Ferrofluids?
Dipolar magnetic fluids (also known as ferrofluids or ferrocolloids), are colloidal suspensions of ferromagnetic nanoparticles (typical sizes 10-20nm), usually stabilised by steric coatings (in non electrolyte carrier liquids) or by electrical double layers (in aqueous solutions). Sterical coatings are usualy made of a stabilizing dispersing agent (surfactant) which prevents particle agglomeration even when a strong magnetic field gradient is applied to the ferrofluid. The surfactant must be matched to the carrier type and must overcome the attractive van der Waals and magnetic forces between the particles. A typical ferrofluid may contain by volume 5% magnetic solid, 10% surfactant and 85% carrier.

Due to their size, ferrofluid particles can be considered as magnetic single-domains with a permanent magnetic moment proportional to their volume.
To know more about the basics of ferrofluids, see for instance the ferrofluids in the Wikipedia.
Synthesis of ferrofluids
The idea of making a liquid with magnetic properties seems to date back to the 1779 when Gowan Knight tried to make a magnetic fluid by introducing iron filings into water. Unfortunately, the iron filings sedimented very quickly. In the XX century the issue was retaken by F. Bitter (1932), and W.C.Elmore (1938), but the particles they obtained were quite large and not fully stable. It seems that Stephen Papell Solomon (US Patent 3215572 ) working for NASA in the 60s was the first to develop an easy and effective way of preparing such colloidal systems. The idea was to be able to use these particles to control the flux of fuel in a zero gravity environment. Since then, many synthesis have been developed to produce ferrofluid particles in both non-polar and polar solvents, increase their stability, improve the control over their size and degree of polidispersity, and produce particles with different materials and shapes. For recent reviews about the subject see (Lu2007) and (Tourinho1998).
You can also prepare your own ferrofluids and have fun at home! See for instance the educational article of Berger et al. (Berger1999), as well as the following link.
Why are Ferrofluids interesting?
Ferrofluids are interesting for a two fold reason:
Ferrofluids are systems exhibing anisotropic interactions leading to a very reach phase behaviour, as well as very interesting rheological and magnetic properties. Thus ferrofluids are a paradigma of physical systems with anisotropic interactions.
The singular properties of ferrofluids in external magnetic fields have found application in many areas, ranging from engineering, to biomedical applications (Popplewell1984,Rosensweig1985, Odenbach2002, Alexiou2003,Hilger2004, Scherer2005). Just to mention a few examples:
Magnetic Seals for instance in vaccum pumps and ferrofluid bearings.
Car dampers
nanoactuators
adaptive optics (liquid mirrors)
biologically inspired robots.
Cancer treatment, cell separation, ultrasensitive analysis, MRI.
Art.
Aggregating structures formed by Ferrofluids
Even in the absence of external fields, ferrofluids have a very complex microstructure, which is caused by the combination of interparticle interactions specific to magnetic fluids (see for instance figures 1 and 2). Ferrofluid particles are known to self-assemble into a variety of magnetic equilibrium structures which depend on several factors such as: system geometry, magnetic interactions, particle polydispersity, presence or absence of external fields, etc.
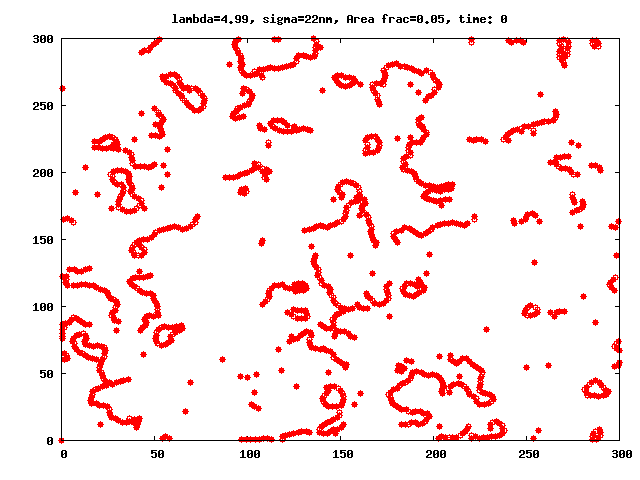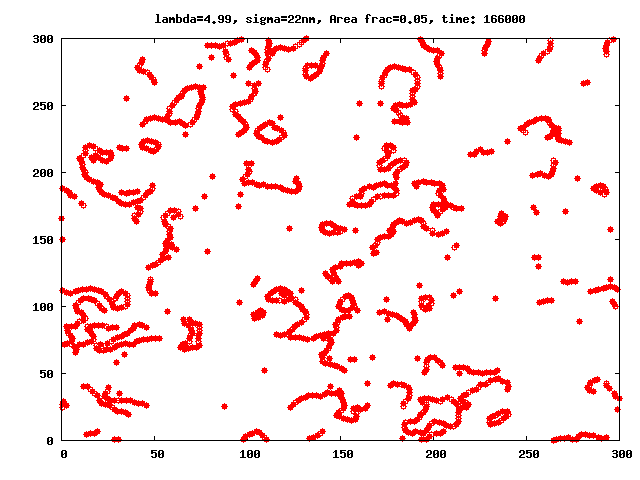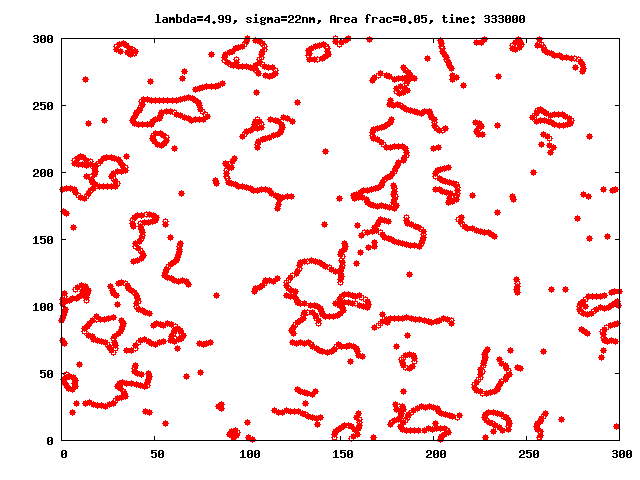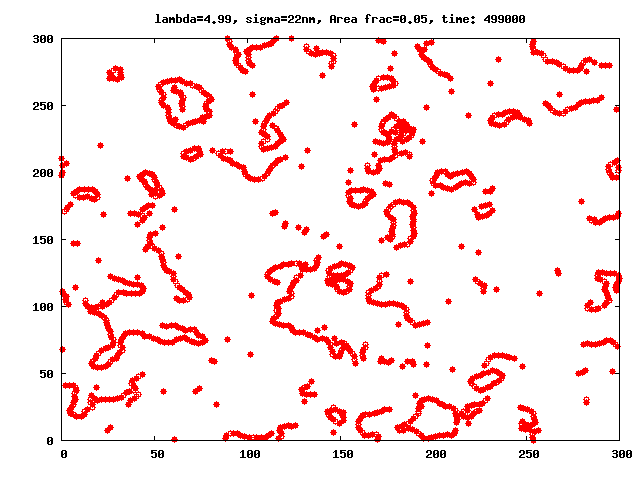
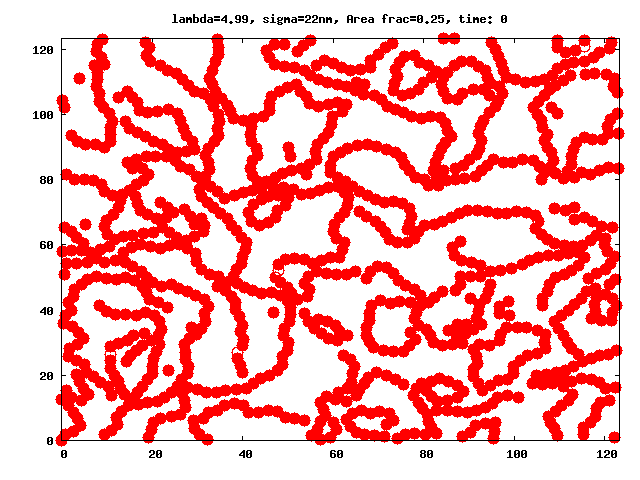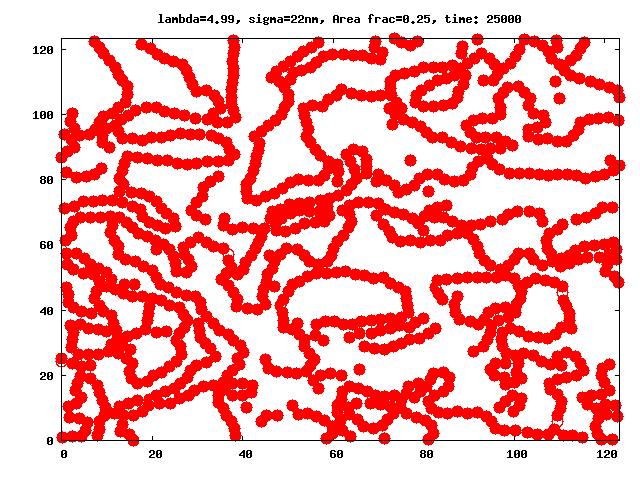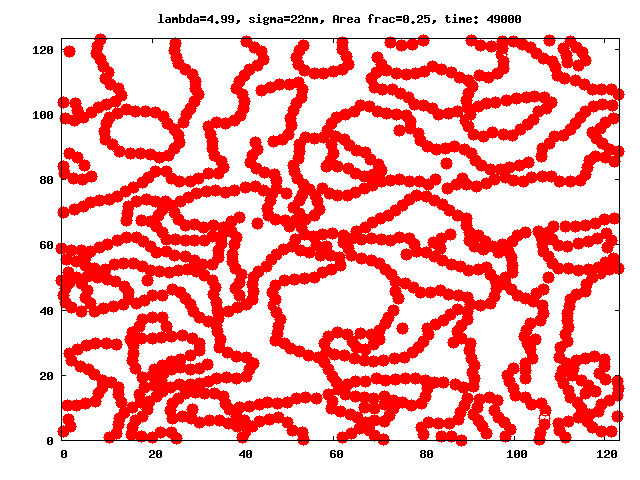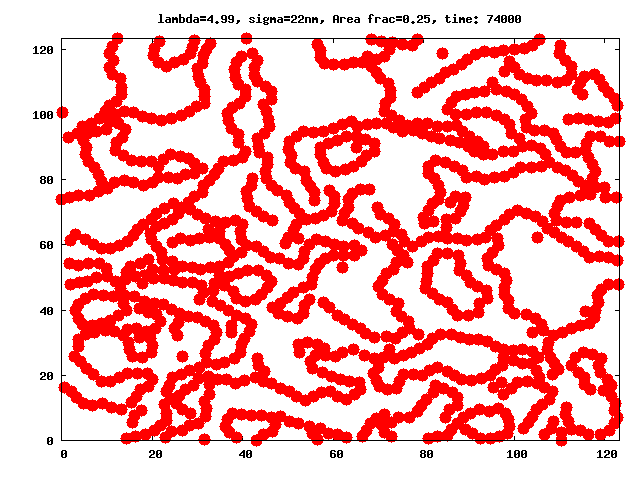
The number of probable cluster topologies in magnetic fluids is high: drops with high magnetic phase concentration (micron size), branched and fractal clusters (hundreds of nanometers in size), or chain- and ring-like structures (tens of nanometers). Signs of clustering process in ferrofluids at zero field are known for more than 40 years (Hess1966). Nonetheless, despite the large amount of clues obtained in subsequent studies (Shen2001, Donselaar1999, Cebula1983, Gazeau2002), a direct experimental proof of the existence of clusters like chains, rings, etc. has been elusive for many years, specially for those cases were dipole-dipole interactions were relatively week, like in magnetite nanoparticles (Fe3O4). Thus, due to the lack of conclusive experiments, the understanding of how dipole-dipole interactions influence the clustering process and determine the subsequent microstructure and phase behaviour of ferrofluids has become a challenge. In bulk ferrofluids, those aspects have been studied in detail through theoretical (Gennes1970, Jordan1973, Osipov1996, Zubarev1995, Tavares1997, Tavares1999, Roij1996, Tlusty2000, Morozov2002, Mendelev2004, Ivanov2004) and simulation (Weis1993, Levesque1994, Jund1995, Camp2000, Pshenichnikov2000, Wang2002, Wang2003, Holm2006) works. Comprehensive reviews on these subject for bulk systems are also available, see (Teixeira2000, Cabuil2000, Huke2004, Holm2005).
Ferrofluid Monolayers
The phase behaviour and microstructure of ferrofluid systems in reduced dimensions is not necessarily equivalent to that of 3D systems. In addition, thin-films and monolayers, have become recently a more successful experimental scenario to assert the existence of the clustering process (Klokkenburg2006, Butter2003, Puntes2001, Wen1999). In the experiments of Philipse and co-workers(Butter2003, Klokkenburg2006), images obtained by cryogenic transmission electron microscopy (cyro-TEM) give ample evidence of the existence of chain- and ring-like structures in ferrofluid monolayers, where all particles are trapped in one plane, but their magnetic moments are free to fluctuate in 3D (q2D monolayers).
In recent years, several theoretical and computational works have been devoted to the study of ferrofluids in monolayers and thin-films. The thermodynamics, and magnetisation properties of quasi-two-dimensional (q2D) systems have been studied by Lomba et al. (Lomba2000), and Gao et al. (Gao1997). Weis and co-workers (see (Weis2002b, Weis2003), and references therein), have performed Monte Carlo simulations of monolayers and systems of finite thickness involving dipolar interactions. They have shown that q2D dipolar systems, alone or in combination with other interactions, present a rich variety of structures, phases and phase transitions. In a recent q2D Monte Carlo study on dipolar hard spheres (DHS), Tavares et al. (Tavares2006) have reported the structure of the fluid to be well described by an ideal mixture of self-assembling clusters at low and intermediate densities. Very recently, Duncan-Camp (Duncan2006) have studied the kinetics of aggregation in monolayers using stochastic dynamics simulations. The results obtained in that work suggest that the conditions for defect-driven condensation (Tlusty2000) could be met by kinetic trapping, giving rise to a metastable phase transition between isotropic fluid phases. The structure formation and magnetic properties of polydisperse ferrofluids in monolayers have been also recently addressed by theory and Monte Carlo simulations (Morimoto2003, Aoshima2004, Kristof2005).
Current Research
Despite the progress obtained in previous studies, the understanding of the phase behaviour and microstructure formation of ferrofluids in constrained geometries is only partial. The understanding of such features is of paramount importance in order to know better those systems and reduce the large amount of times devoted to trial-error in order to improve or design new applications based on ferrofluids.
Our interest has focused on the peculiarities of the aggregation processes in both quasi-two dimensional (monolayers) [23] [25] [29] [45] [47] and bulk ferrofluid systems [35]. We make use of a combination of density functional theory, and molecular dynamics (MD) simulations. The microstructure formation and phase behaviour are studied thoroughly through a comparison of the theoretical, and computational results. The active areas of research about ferrofluids in our group at this moment are:
(1) Ferrofluid monolayers: monodisperse particles.
Non Branched systems
We investigate the peculiarities brought by the Quasi-2D geometry into the aggregation ferrofluid microstructure in particular in the range of parameters for which the chain-like structures have been observed implicitly or explicitly in 3D experiments, simulations and theoretical models. In difference to previous papers studying aggregates in q2D monolayers, we focus our attention on the detailed analysis and extensive comparison of the results coming from MD simulations with a newly developed theoretical approach, which give us cluster sizes and distributions as functions of the magnetic interaction and area fraction of ferroparticles in monolayers.
A thorough comparison of the predictions of the theory with the values obtained through equilibrium Molecular Dynamic simulations have shown that: in the range of the space of parameters λ (dipolar coupling), and area fraction φ in which the theory could be expected to be valid (regions with low number of branched structures), the theory is able to closely predict the simulation results, and allow us to calculate the partition functions for these clusters in constrained geometries and describe the influence of the latter constraints on the entropy of a ferrofluid.
The comparison shows that excluded area interactions play a crucial role in quasi 2D, where the constrains imposed by the Q2D monolayer geometry change the entropy of clusters. The refinement of the present theory by dropping out several of the limiting constraints is currently being worked out.
Branched and Network systems
At high values of the dipolar coupling and area fraction parameters, the systems exhibit kind of network and branched structures which are currently characterized via simulation and theory.
(2) Ferrofluid monolayers: bidisperse particles.
In the case of bidisperse particles we have two different kind of particles that differ in their size, and therefore in the strength of the magnetic interaction. We are studying the dependence of the microstructure of clusters in a monolayer on the relative size as well as ratio of concentrations of small and large particles in the system. The possible existence of Poissoning and anti-poissoning effects in those systems are under investigation. A comparison of theoretical and numerical results against experimental results has been performed [36].
(3) Structure factors of ferrofluids in the low-density low-aggregating limit.
The Structure factors of ferrofluids at low-densities in the regime of low values of the dipolar coupling parameter λ have been studied in absence and in presence of magnetic fields [31] [38]. The performance of theoretical formalisms predicting such structure factors are currently being assesed using numerical simulations.
(4) Magnetic particles with shifted dipoles.
Our studies of particles which possess a dipole momenth that is shifted out of the center of mass, towards the surface, have revealed that such kind of particles exhibit a very differen behaviour respect to traditional particles in which the dipole is assumed to be located at the center of the particle [30] [32].
Collaborators
Prof. Dr. Sofia Kantorovich (Vienna University)
References
[Alexiou2003] Alexiou Ch, Jurgons R, Schmid R, Bergmann C, Henke J, Huenges E, and Parak F , J. Drug Target, (11), 139, (2003).
[Aoshima2004] Aoshima M, Satoh A, J. Coll. Int. Sci., (280), 83, (2004).
[Berger1999] Berger P, Adelman NB, Beckman KJ, Campbell J, Ellis AB, and Lisensky GC, J. Chem. Education, (76), 943, (1999).
[Butter2003] Butter K, Bomans PH, Frederik PM, Vroege GJ, Philipse AP, J. Phys.: Condens. Matter, (15), S1451, (2003).
[Cabuil2000] Cabuil V, Curr. Opin. Colloid Interface Sci., (5), 44, (2000).
[Camp2000] Camp PJ, Patey GN, Phys. Rev. E, (62), 5403, (2000).
[Cebula1983] Cebula DJ, Charles SW, and Popplewell J, J. Physique, (44), 207, (1983).
[Donselaar1999] Donselaar LN, Frederik PM, Bomans PH, Buining PA, Humbel BM, and Philipse AP, J. Magn. Magn. Matter, (201), 58, (1999).
[Duncan2006] Duncan PD, Camp PJ, Phys. Rev. Lett., (97), 107202, (2006).
[Gao1997] Gao GT, Zeng XC, and Wang W., J. Chem. Phys., (106), 3311, (1997).
[Gazeau2002] Gazeau F, Dubois E, Bacri JC, Boue F, Cebers A, and Perzynski R, Phys. Rev. E, (65), 031403, (2002).
[Gennes1970] de Gennes PG, and Pincus PA, Phys. Kondens. Matter.,(11), 189, (1970).
[Hess1966] Hess PH, and Parker PH, J. Appl. Polym. Sci. (10), 1915, (1966).
[Hilger2004] Hilger I, Andrä W, Hergt R, Hiergeist R, and Kaiser W A, Inorganic Materials, Recent Advances ed D Bahadur, S Vitta, and O. Prakash (2004, New Delhi: Narosa Publishing House).
[Holm2005] Holm C, Weis JJ, Curr. Op. Coll. Int. Sci., (10), 133, (2005).
[Holm2006] Holm C, Ivanov A, Kantorovich S, Pyanzina E, Reznikov E, J. Phys.: Condens. Matter, (18), S2737, (2006).
[Huke2004] Juke B, and Lücke M, Rep. Prog. Phys., (67), 1731, (2004).
[Ivanov2004] Ivanov AO, Wang Z., and C. Holm, Phys. Rev. E, (69), 031206, (2004).
[Jund1995] Jund P, Kim SG, Tománek, and Hetherington J, Phys. Rev. Lett., (74), 3049, (1995).
[Pshenichnikov2000] Pshenichnikov AF, and Mekhonoshin V, J. Magn. Magn. Mater, (213), 357, (2000).
[Jordan1973] Jordan PC, Mol. Phys., (25), 961, (1973).
[Klokkenburg2006] Klokkenburg M, Dullens RPA, Kegel WK, Erné) BH, Philipse AP, Phys. Rev. Lett., (96), 037203, (2006).
[Kristof2005] Kristóf T, Szalai I, Phys. Rev. E, (72), 041105, (2005).
[Levesque1994] Levesque D, Weis JJ, Phys. Rev. E, (49), 5131, (1994).
[Lomba2000] Lomba E, Lado F, Weis JJ, Phys. Rev. E, (61), 3838, (2000).
[Lu2007] An-Hui Lu, E. L. Sabas, and Ferdi Schüth, Angew. Chem. Int. Ed., (46), 1222, (2007).
[Mendelev2004] Mendelev VS, and Ivanov AO, Phys. Rev. E, (70), 051502, (2004).
[Morozov2002] Morozov KI, and Shliomis MI, 2002, Ferrofluids, Magnetically Controllable Fluids and Their Applications), Lect. Notes Phys., Springer, Berlin, 2002. Ed. Odenbach S.
[Morimoto2003] Morimoto H, Maekawa T, Matsumoto Y, Phys. Rev. E (68), 061505, (2003).
[Odenbach2002] Odenbach S (Ed.), Ferrofluids, Magnetically Controllable Fluids and Their Applications, Lect. Notes Phys., Springer, New York, 2002.
[Osipov1996] Osipov MA, Teixeira PIC, and Telo da Gama MM, Phys. Rev. E, (54), 2597, (1996).
[Popplewell1984] Popplewell J, Phys. Technol.,(15), 150, (1984).
[Puntes2001] Puntes VF, Krishnan KM, and Alivisatos AP, Science (291), 2115, (2001).
[Roij1996] van Roij R, Phys. Rev. Lett., (76), 3348, (1996).
[Rosensweig1985] Rosensweig RE, Ferrohydrodynamics (Cambridge University Press, Cambridge, 1985).
[Scherer2005] Scherer C, Figueiredo AM, Brazilian J. of Phys., (35), 718, (2005).
[Shen2001] Shen L, Stachowiak A, Fateen SK, Laibinis PE, and Hatton TA, Langmuir, (17), 288, 2001.
[Tavares1997] Tavares JM, Telo da Gama MM, and Osipov MA, Phys. Rev. E, (56), R6252, (1997).
[Tavares1999] Tavares JM, Weis JJ, and Telo da Gama MM, Phys. Rev. E, (59), 4388, (1999).
[Tavares2006] Tavares JM, Weis JJ, Telo da Gama MM, Phys. Rev. E, (73) 041507, (2006).
[Teixeira2000] Teixeira PIC, Tavares JM, and Telo da Gama MM, J. Phys.: Condens. Matter, (12), R411, (2000).
[Tlusty2000] Tlusty T, Safran SA, Science (290), 1328, (2000).
[Tourinho1998] Tourinho FA, Braz. J. Phys. (28), doi:10.1590/S0103-97331998000400016, (1998).
[Wang2002] Wang Z, Holm C, and Müller HW, Phys. Rev. E, (66), 021405, (2002).
[Wang2003] Wang Z, Holm C, Phys. Rev. E, (68), 041401, (2003).
[Weis1993] Weis JJ, Levesque D, Phys. Rev. Lett., (71), 2729, (1993).
[Weis2002b] Weis JJ, Tavares JM, and Telo da Gama MM, J. Phys.: Condens. Matter, (14), 9171, (2002).
[Weis2003] Weis JJ, J. Phys.: Condens. Matter, (15), S1471, (2003).
[Wen1999] Wen W, Pál KF, Zheng DW, and Tu KN, Phys. Rev. E, (59), R4758, (1999).
[Zubarev1995] Zubarev AY, and Iskakova LY, J. Exp. Theor. Phys., (80), 857, (1995).
Magnetic Filaments and magnetic polymer brushes
What are magnetic filaments and magnetic colloidal polymers?
Artificial magnetic filaments (also known as magnetic colloidal polymers) can be obtained by mutually linking magnetic colloids to form a chain. These magnetic chains represent the equivalent to magnetic polymers but at supra-molecular scale. In difference to one-dimensional chemical magnetic polymers which only manifest their magnetic properties at temperatures below 100K, magnetic filaments can retain their magnetism at room temperature and zero field. In addition to this single polymeric units, there exist a related family of systems in which many magnetic filaments are attatched by one of their ends to a surface, creating a system similar to polimeric brushes but at the supra-molecular scale. These systems are known as magnetic colloidal brushes.
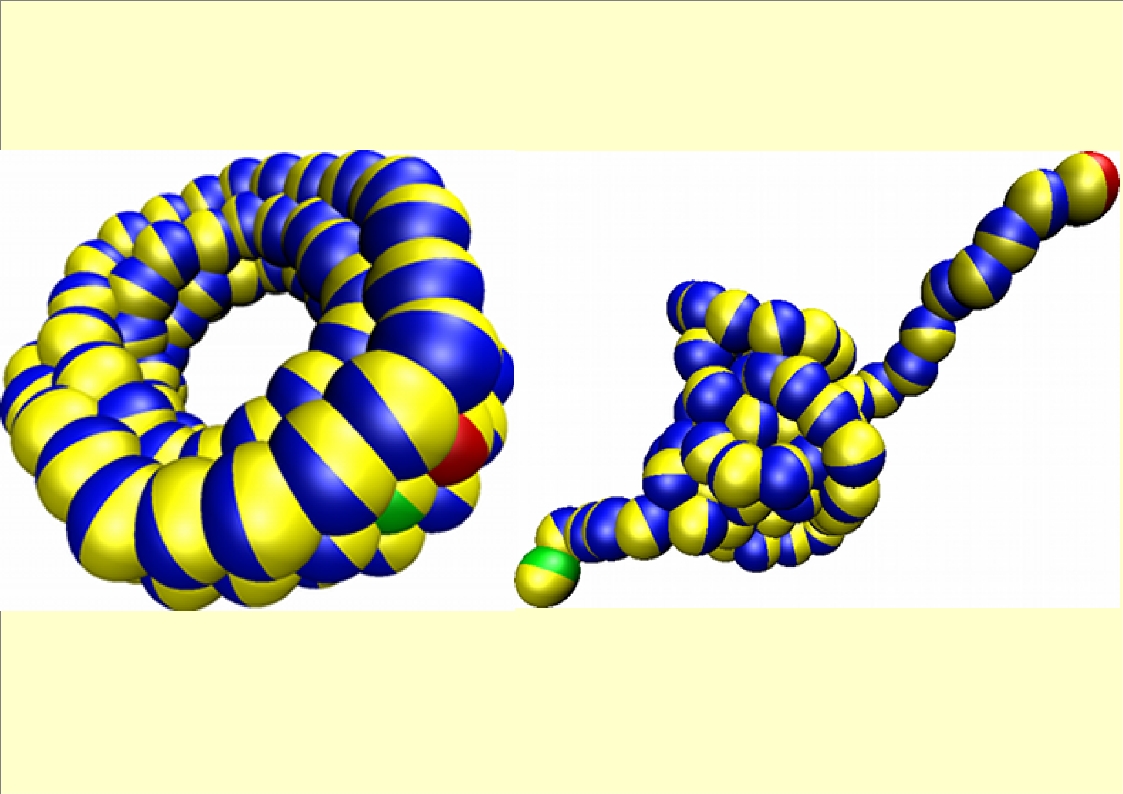

What are they useful for?
The emerging interest in this relatively novel field is due to the fact that magnetic filaments are very appealing from the technological point of view. They can be thought as improved substitutes of current ferrofluids, or as elements for magnetic memories, chemical and pressure nanosensors, micro-propellers, non-permanent photonic crystals, and generation of unique patterns able to provide watermarks to authenticate cards or other documents, to just mention a few.
Our research
In a first step our reseach on the topic focused on the equilibrium conformations of flexible and semiflexible magnetic filaments in different physical environments of relevance for forthcoming applications [19] [12]. In particular, we studied the determination of the phase diagram at zero field for magnetic filaments where their monomers exhibit short-range LJ attractive interactions (Stockmayer polymers, i.e. filaments in poor solvent conditions) in the limit of strong dilution, as well as filaments in good solvent conditions. We studied the cases of magnetic chains in bulk and near an attractive surfaces [26] [9]. We find that the phase diagrams of magnetic systems exhibit a rich variety of new phases when compared with non-magnetic chains in similar environments.
In a subsequent stage of our research we paid attention to the conformational behaviour of magnetic polymer brushes, in the absence and presence of external fields [16] [17] [18] [21] [22]. Among many interesting results we found that the magnetic content [7] of the filaments is a key element in controlling the extension of the filaments towards the bulk: there exist an optimal content of magnetic matter that optimizes the extensibility of the brushes at a given constant external field strength. We also have studied the structure factors and the internal structure of filament brushes [13] which turned out to be much complex than in neutral brushes bein strongly anisotropic in the direction perpendicular to the grafting surface.
In a next step in our research was the study of magnetic filaments in flow in the limit of infinite dilution [15] [10] [6] [2] and in the case of finite concentration suspensions [11]. Later we analyzed the behaviour of magnetic brushes inside narrow slits. We investigated the use of external fields not only to control the conformations adopted by the brushes inside such highgly confined spaces, but also how such changes in conformation could be used to modify the flow of binary-size distribution mixture of colloids. We found that we could use these systems to separate the particles of different size, which has a large potential to build up controlable-columns for size exclusion chromatography [10].
More recently we have focused on the study of the use of magnetic filaments as depletant agents for colloidal suspensions [5] which induced depletion forces can be externally tuned by using a magnetic field. We have found that as a function of the strength of the external field these systems can lead to a funnel effect to link colloidal particles sequentially in a row, as well as to stationary points between particles which can be used as a sort of “magnetic tweezers” to control de effective distance between colloidal particles. We have focused so far in 2D depltant systems so far, but we plan to expand our research toward full 3D systems. The reason why these magnetic polymeric systems can lead to depletion forces not seen in neutral polymers is due to the exsitence of Kelvin Forces that arise from the permeability mismatch between the large colloidal particles and the magnetic colloidal polymers.
Encouraged by the observed effect of Kelvin Forces on traditional depletion forces, we decied to investigate the case of the force that a magnetic colloidal brush exerts on a non-magnetic particle that tries to approach the brush [4]. Our results show that in this case Kelvin Forces exert an attractive force between the surface on which magnetic filaments are anchored and the large non-magnetic colloidal particle that approaches the brush. This attractive force opposes the traditional steric repulsive force that any polymeric brush will exert on approaching particles. Via external fields one can tune the strength of this attractive forces creating a region of a high repulsion barrier at large distances from the brush and at very short distances, while an intermediate region in which attraction between the colloidal particles and the grafting surface exists. In this attractive region a stationary point may develop which implies that once the initial repulsive barrier is overpassed, the particle may be retained inside the brush. As the stationary point and the repulsive barrier depend on the strength of the external field and the size of the penetrating particle, these systems have the potential to be used in many different applications: from enhanced catalysis systems and drug delivery, to cell sorting and chromatography. It also provides us with clues about how endothelial glycocalyx behaves.
It’s worth to mention, that although our research has been done using magnetic dipoles, similar results must be expected for their elctric dipolar counterparts, as the dipole-dipole interaction and Kelvin Forces are similar except for some factors.
Collaborators
Prof. Dr. Sofia Kantorovich (Vienna University)
Prof. Dr. Pedro Sánchez (Vienna University)
Polyelectrolytes and Polyelectrolyte Multilayers
Polyelectrolytes (PE1 ) are polymers that contain moieties which exhibit a certain degreeo of charge. Many biological polymers like for instance proteins, DNA or glycosyaminoglycans are polyelectrolytes. In our group we have experience on dealing with those systems. Thus for instance we have performed studies combining experiments and numerical simulations on the formation of complexes between cationic-like charged polyelectrolyes and surfactants [14], for which we have observed that the addition of tetravalent salts plays a key role in the formation of such complexes formed by elemets with the same type of charge.
Another very interesting area of research in the field of polyelectrolyes we have pursued in our group is the formation of Polyelectrolye multilayers.
What is a Polyelectolyte Multilayer (PEM)?
Self-assembly processes of charged polymers known as polyelectrolytes can be used to build-up multilayered materials (PEM) with unique properties. In the early 90’s Decher et al [B1] demonstrated the feasibility of the self-assembly of polyelectrolyte multilayers (PEMs) using the so-called Layer-by-Layer (LbL) technique.
Why Polyelectrolyte multilayers are interesting?
The versatility of the LbL process has allowed the fabrication of thin multilayer films made of synthetic polyelectrolytes, DNA, lipids and proteins, which has resulted in a boost of novel applications in recent years. For instance, PEMs are used as matrix materials for enzymes and proteins in sensor applications [B2], and also as a matrix for active components in solar cells. PEMs are used as a coating for protecting and control the healing process of damaged arteries [B3]. In addition PEM’s can be used as permeable membranes for nanofiltration [B4], gas separation, and fuel cells. Furthermore, PEM’s are also used in the fabrication of non-linear optical materials [B5], coloured electrochromic electrodes (future display devices), and to tailor the properties of photonic crystalls [B6]. Other uses of PEM’s include analyte separation processes (chromatography) [B7], and the fabrication of thin-walled hollow micro- and nanocapsules (see [B8], and ref. therein). These capsules have great potential for drug carrier and nanoreactors.
Status of the PEMs research at a glance
Since the pionering work of Decher et al in the 90s, many scientists have been studying and characterizing the properties of Polyelectrolyte Multilayers. The research done about PEMs has been summarized in a few reviews [B9-B13]. But, just to mention a few relevant contributions to the field of PEM´s:
PEM experimental studies.
Experiments have established several important features for PEM’s: the thickness of each adsorbed layer shows almost a linear dependence on the salt concentration. Flexible polyelectrolytes in two component multilayers are known to intermix over several adjacent layers. This layer intermixing can be suppressed by using more rigid blocks for the assembly [B13]. Intrinsic charge compensation by polyions accompanied by overcharging and the kinetically irreversible nature of deposition has also been reported.
In the case of weak polyelectrolytes, very interesting variations of the stability, the thickness, the stiffness, the permeability and the porosity of PEMs have been observed by adjusting the pH of the dipping solutions; this change not only modifies the new layers, but also has an effect on previously adsorbed layers [B14]. The measurements of the Young’s modulus of PEMs show a strong correlation with [ionomers] , and therefore it could be possible that the structure of PEMs is close to that of ionomers. The role that the charge density of the PE plays on PEMs growth is somewhat unclear. Despite the existence of considerable data in the literature concerning the influence of the charge density on PEM formation, there is little consensus, and conflicting results have often been reported [B15]. As an example of such controversy, some works have reported the existence of a critical minimum charge density below which is not possible the formation of PEMs whereas other works have observed multilayer buildup with PE of very low charge density [B15].
From the extensive research over the past few years on PEMs, it is clear that unlike single layer films or polymer gels there is no general description of the physicochemical properties of different PEMs systems, especially for those assembled from weak polyelectrolytes. Another clear example of the previous claim is found in the buildup mechanism of PEMS [B16]: whereas strong polyelectrolytes usually observe a linear growth for the PEM’s thickness, weak polyelectrolytes do not always follow this pattern and can exhibit an exponential growth. The assembly conditions, even in the case of using the same PE, can modify the buildup regime. Thus, for instance, it has been shown very recently that an increase in temperature has a profound influence on the rate of the layer-by-layer buildup [B17]. Furthermore, an elevated temperature is shown to swap the buildup from a linear to an exponential regime. The exact mechanism behind the phenomenon of the nonlinear growth is unknown at present. There are studies that suggest the surface roughening as responsible of the exponential growth (see ref. in [B18]). Instead, other models are concerned with a certain active volume of the PEM, or the diffusion of polyions in and out of the film (see ref. in [B17]). Another example of the complexity of the behaviour of weak PE is the shift in the charge density of weak PE depending on if they are adsorbed to the PEM or remain in solution. Furthermore, recent experimental reports ([B18] and ref. therein) suggest that non-electrostatic short-range interactions, like for instance the hydrophobic interaction, also play an important role in the multilayering process. Moreover, it has been reported that the structures formed usually are metastable at some film buildup stages and little knowledge exist about the film relaxation during these stages.
PEM theoretical studies.
There have been very few attempts to describe theoretically the electrostatic self-assembly, and all of them are build-up on severe assumptions hard to test experimentally; specifically they assume that PEM are equilibrium structures. Netz and Joanny [B19] considered the formation of multilayers in a system of semiflexible polyelectrolytes (PE), assuming that the deposited layer structure was fixed, providing a solid charged substrate for the next layer. Mayes et al [B20] applied a similar idea to flexible PE. Both these models neglect interpenetration (interdigitation) and chain complexation between the layers, which are usual features found in experimental works about PEMs. The oppositely limit of strong intermixing of PE between neighbouring layers was considered by Castlenovo and Joanny [B21] by incorporating the complex formation between oppositely PEs into self-consistent field equations. Unfortunately this equations are limited to solutions of high ionic strength, were electrostatic interactions can effectively be treated as short-range interactions. Despite these huge efforts, the strong correlations existing between oppositely charged polyions, provides a formidable challenge for their theoretical description. In this respect, numerical simulations could be of great help.
Numerical simulations about PEMs.
There exist few computational studies about electrostatic self-assembly of PEM. In a seminal paper on layer formation on a spherical substrate [B22] it has been demonsrtated that additional non-electrostatic forces are needed to produce nice PEMs. This suggests that multilayering is possibly not an equilibrium phenomenon evidence of which has been also observed experimentally [B23]. Similar conclusions have been drawn for other geometries using either Molecular Dynamics (MD) or Monte Carlo (MC) techniques [B24, B25]. Another outcome is, that these studies have confirmed the fuzzy nature of PEMs (molecules in one layer interpenetrate other layers) , although almost perfect periodic oscillations of the density differences between monomers belonging to positively and negatively charged PE have been found. MC studies (see refs. in [B26]) have reported stability as well as the microstructure of the PE layers to be especially sensitive to the strength of the non-electrostatic short range attraction between the PE and the charged substrate. In addition, the thickness of the adsorbed layer is observed to decrease when increasing PE concentration or surface charge density, although the total adsorbed amount displays a non-monotonic dependence on polymer concentration. It was also demonstrated that the formation of multilayers as well as the extent of layer intermixing depends on the molecular weight of the PE chains and the fraction of charge on its backbone. The presence of ionic pairs between oppositely charged PE that form the layers have been claimed as a possible important factor in stabilizing the multilayer films. In the last years, MD studies for the assembly of flexible PE onto flat charged surfaces [B26] have suggested the formation of thermodynamically stable structures from bulk mixture solutions. This is a controversial, very basic issue that opposes to some experimental reports, and certainly needs to be clarified.
Our Research
In spite of the amount of work done during the last 30 years, the understanding of the multilayer formation process and the knowledge about how slight differences during the growth process are able to strongly modify the properties of the multilayer materials is still in its infancy. The complex nature of PEMs possesses a challenge when one tries to choose a PEM system for a particular application. Therefore, one must first try to learn more about the fundamental properties of PEMs before it is possible to understand how to use these films for specific applications without a large and exhausting process of trial and error. Doubtless, the understanding of such issues is of paramount importance to improve current building-up methods and devices, tune finely the properties of such materials for specific purposes, and in turn devise new potential applications for such materials. Such knowledge will not be only of benefit for the Scientific Community but also for industry as well as society due to the huge potentiality of such materials for new devices and applications.
Our reserach on Polyelectrolyte Multilayers (PEMs) has been aimed to help to shed light on some still not clearly understood aspects governing multilayer formation and the control of their properties [34] [37] [40] [42]. At this stage, numerical simulations that use the state-of-the-art algorithms to deal with charged soft matter offer a very valuable and useful tool in order to elucidate the mechanisms governing multilayering assembly and the properties of PEMs. These numerical simulations can build a bridge between the detailed experimental results and the relatively coarse grained analytical models. Our current aims in the area of PEM research are:
Clarify which factors contribute to stabilize multilayer films with special reference to weak polyelectrolytes.
Explain the mechanisms and the causes that induce the formation of exponential growing films instead of linear films.
Study how the stability and the properties of PEMs, as well as the kinetics of both linear and exponential buildup regimes as a function of the several factors which have been observed to be of relevance in experiments.
Study of hollow spherical PEM nanocapsules as drug carriers and chemical nanoreactors.
Refine current electrostatic methods in order to allow faster and more detailed simulations of large PEM systems.
Determine, in close collaboration with simultaneous experimental investigations (Specially groups of von Klitzing, T. Hugel, Helm), the inner structure and dynamics of a well defined, but small number of multilayer polymers on various substrates.
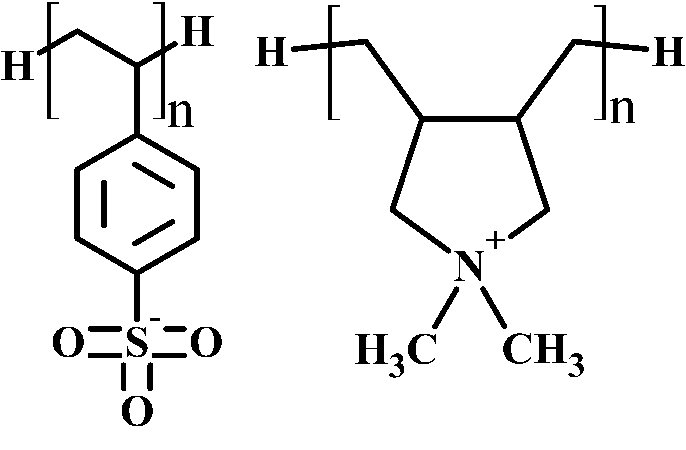
More specifically, we are currently studying the inner structure and dynamics of a small layer number of PEMs via all-atom (AA) and coarse-grained (CG) simulations. The AA level simulations have proved to be consistent with existing experimental data on chain conformation of adsorbed poly(styrene sulfonate) (PSS) in PSS monolayer systems, dielectric permittivity and diffusion constant of water in PSS/PDADMA polyelectrolyte complexes (PDADMA stand for poly(diallyldimethylammonium)).
We have built the PSS/PDADMA bilayers based on the previously obtained PSS monolayers and we are expecting to extract exciting information from these studies. The simulation of a bilayer represents our final goal for atomistic simulations of PMEs so far, due to the high requirement of computer resources (ca. 1000 000 cpu hours in total).
Due to the limitations of atomistic simulations, further insight into structure and dynamics of PEMs can be achieved only with simulations at CG level. Qualitative understanding and agreement with experiments has been obtained by us using the already existing generic bead-spring PE model. However, a refined CG PE model is needed in order to be quantitatively predictive. This is part of our next working program.
Some selected results obtained during these last years are:
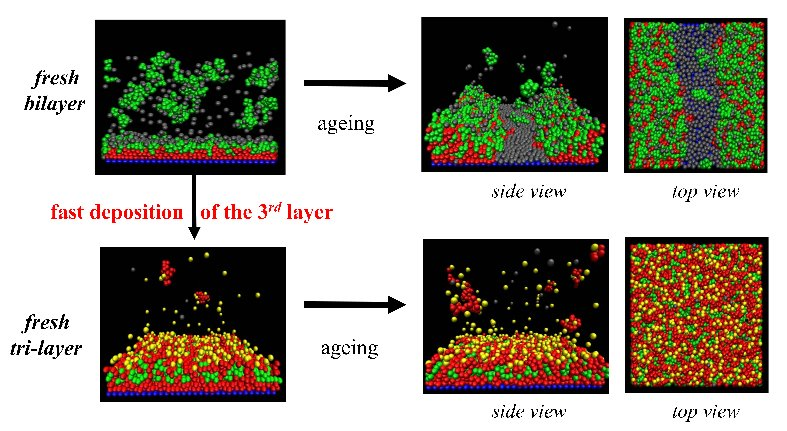
a) Bilayer thermodynamical instability
Our CG level simulations have shown that depending on the relative strength of the monomer-monomer and monomer-surface interaction energies, a progressive redissolution of the first bilayer or a partial dewetting resulting in a disordered melt can happen.
We have shown that a fast enough deposition of the third layer – before the aging process – can prevent such redissolution or partial dewetting and provide the stability needed to form a PEM. We have checked that the deposition of further layers is a stable process. This suggests that the first PE bilayer is not thermodynamically stable, while tri-layers and higher layers are stable, at least within the long run time of our simulations.
b) Charge compensation mechanism
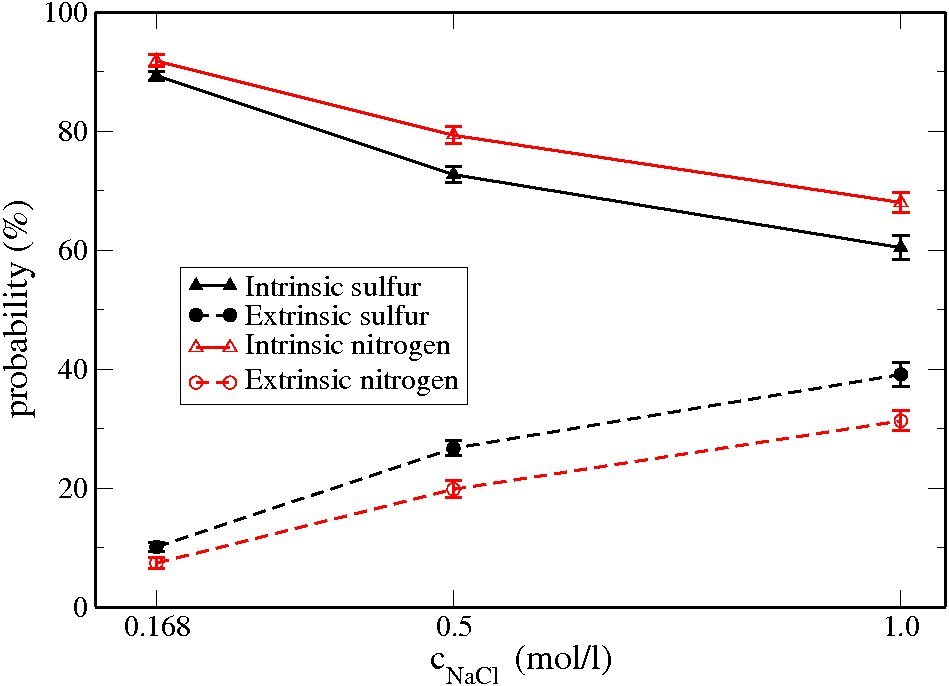
In our AA level simulations on PSS/PDADMA complexes, intrinsic (polyanions pair with polycations) and extrinsic (polyions pair with salt ions) charge compensation mechanisms have been found to co-exist, although the intrinsic one is predominant in the studied salt (NaCl) concentration range from 0.17 to 1.00 mol/L.
Furthermore, the relative scale of the interaction energy of the ion-pairs in such PSS/PDADMA mixture is calculated to follow (in kJ/mol): Na-Cl (-520) > PSS-Na (-420) > PDADMA-Cl (-280) ~ PSS-PDADMA (-270). The relative scale of the interaction energy can be very useful to explain some experimental finding, such as PSS is found to be in a higher concentration than PDADMA in PSS/ PDADMA complexes [5]. This information is also valuable to properly model the interactions between ion-pairs in the upcoming refined CG model.
c) PSS adsorption monolayer
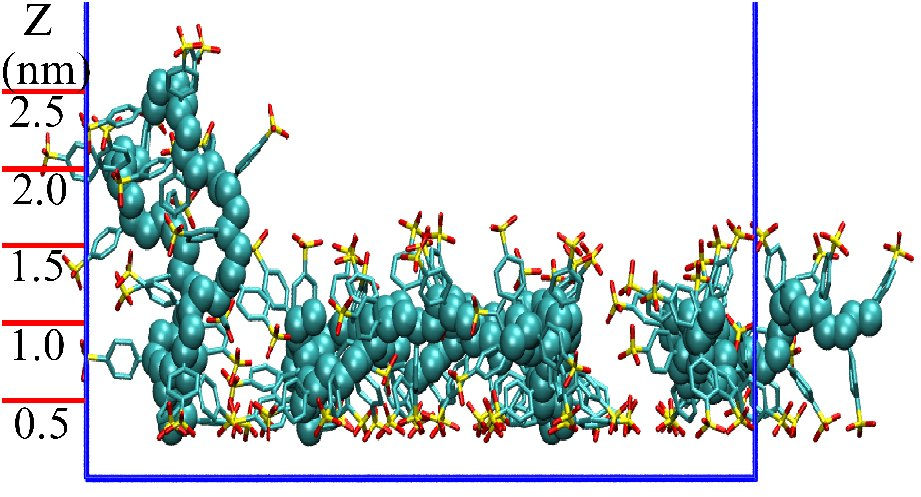
The PSS monolayer is diposited from a PSS solution via atomistic simulations. Our results demonstrate that short-range interactions of van der Waals origin from the adsorbing substrate play a significant role in the layer structure of the adsorbed PSS, and they alone are already sufficient to induce a stable PSS adsorption layer. The PSS chains are found to behave as hydrophilic PEs, two kinds of conformations of which are observed: flat PSS adsorption layer dominates with some adsorbed PSS chains dangling into the above PSS solution.
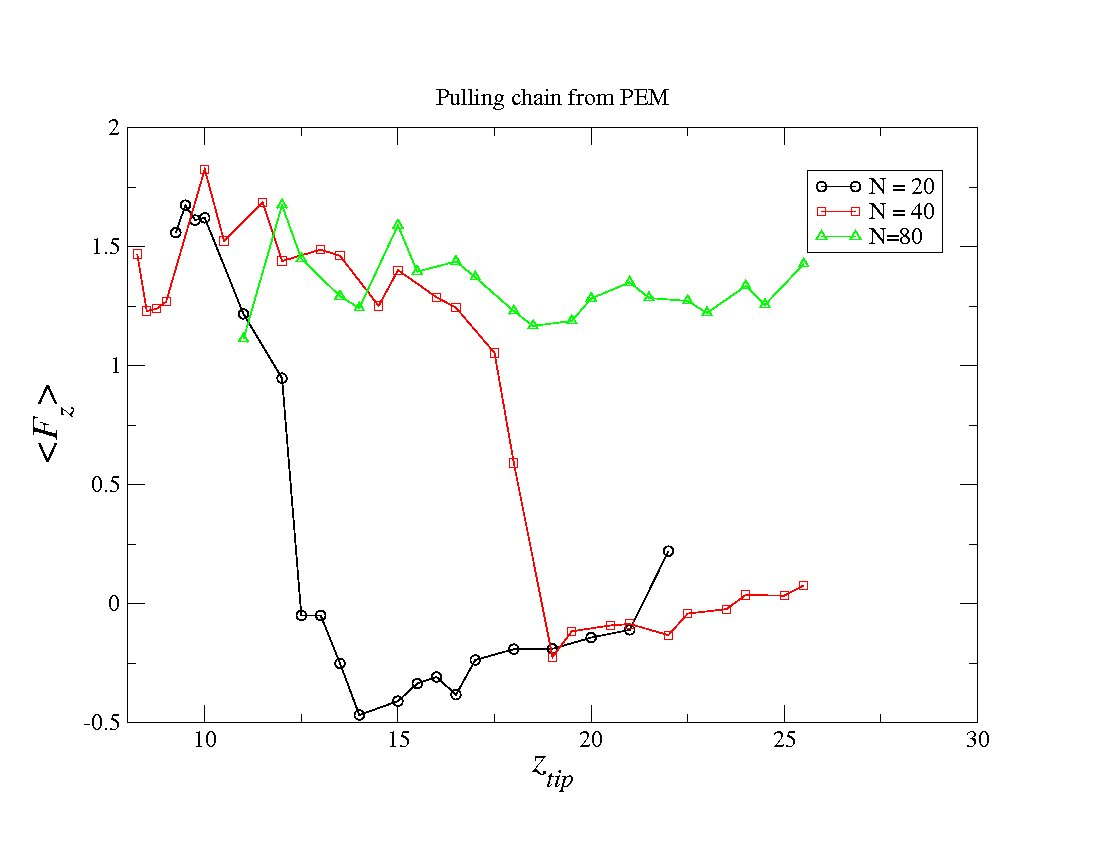
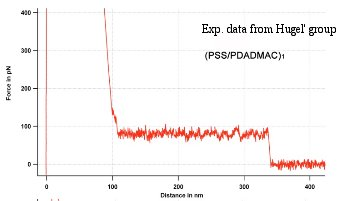
d) PE chain pulling experiment
The present, non-refined CG model yields a qualitative agreement with the experiments by the Hugel group. This makes us confident that maybe even a quantitative comparison might be obtainable once the refined coarse-grained model will be ready.
In the computer simulations on PE pulling experiments, a PE chain, which is similar to the PE chains of the capping layer, is introduced with the corresponding counterions. The averaged force, that is needed to keep one of the chain ends fixed at a given point Z_{tip}, is measured by performing several independent runs. The position of the chain tip is slowly increased to a new value where a new measurement was performed.
Collaborators
References
[B1] J. Schmitt, G. Decher and G. Hong. Thin Solid Films, 1992, 210/211, 831.URL
[B2] Tran D, and Renneberg R, Biosensors and Bioelectronics, 18, 1491, (2003).
[B3] Thierry B, Winnik FM, Merhi Y, and Tabrizian M, J. Am. Chem. Soc., 125, 7494, (2003).
[B4] Malaismy R, and Bruening M, Langmuir, 21, 10587, (2005)
[B5] Jiang L, Lu F, Chang Q, Liu Y, Liu H, Li Y, et al., Chem. Phys. Chem., 6, 481,(2005).
[B6] Arsenault AC, Halfyard J, Wang Z, Kitaev V, Ozin GA, et al., Langmuir, 21, 499, (2005).
[B7] Kamande MW, Fletcher KA, Lowry M, and Warner IM, J. Sep. Sci., 28, 710, (2005).
[B8] Khopade AJ, Arulsudar N, Khopade SA, Hartmann J, Biomacromolecules, 6, 229, (2005).
[B9] Messina R, Holm C, Kremer K, J. Poly. Sci. B, 42, 3557, (2004). [10] Klitzing RV, Wong JE, Jaeger W, and Steiz R, Current Op. Coll. Interf. Sci., 9, 158,(2004).
[B11] Schanhoff M, Current Op. Coll. Interf. Sci., 8, 86, (2003). [12] Hammond PT, Current Op. Coll. Interf. Sci., 4, 430, (2000).
[B13] G. Decher, Science,1997, 277, 1232. URL
[B14] Kharlampieva E, and Sukhishvili SA, Langmuir, 19, 1235, (2003).
[B15] Schoeler B, Kumaraswamy G, and Caruso F, Macromolecules, 35, 889, (2002).
[B16] Kujawa P, Moraille P, Sanchez J, Badia A, Winnik FM, J.Am.Chem.Soc, 127, 9224, (2005) .
[B17] Salomaki M, Vinokurov IA, Kankare J, Langmuir, 21, 11232, (2005). [18] Guyomard A, Muller G, Glinel K, Macromolecules, 38, 5737, (2005).
[B19] Netz RR, Joanny JF, Macromolecules, 32, 9013, (1999).
[B20] Park SY, Rubner MF, and Mayes AM, Langmuir, 18, 9600, (2002).
[B21] Castlenovo M, and Joanny JF, Langmuir, 16, 7524, (2000). [22] Messina R, Holm C, Kremer K, Langmuir, 19, (10), 4473, (2003).
[B23] D. Kovacevic, S. van~der Burgh, M.A. Cohen-Stuart, Langmuir 18, 5607 (2002).
[B24] Patel PA, Jeon J, Mather PT, and Dobrynin AV, Langmuir, 21, 6113, (2005).
[B25] Panchagnula V, Jean J, Rusling JF, and Dobrynin AV, Langmuir, 21, 1118, (2005).
[B26] Abu-Sharkh B, J. Chem Phys., 123, 114907, (2005).
[B27] J. B. Schlenoff, Langmuir, 2009, 25, 14007.URL
[B28] A. V. Dobrynin. Curr. Opin. Colloid Interface Sci, 2008, 13, 376.URL
[B29] H. H. Hariri, and J. B. Schlenoff, Macromolecules, 2010, DOI: 10.1021/ma1012978. URL
Other colloidal and polymeric systems
In addition to colloidal and polymeric systems charged or magnetic, we are also interested in neutral systems. Several of our research works have focused in these systems.
On one side we have studied how colloidal crystallization depends on the strength interaction between colloidal particles [52], and how the structure factor in these aggregating systems will look like [51], which has provided quite a lot of insight to experimentalists.
These studies have been continued by investigating how a sheared flow can help to crystallization in those cases where aggregation does not occur eassily [44] as it happens in the case of some molecules and proteins, which poses an important problem for its determination. We have found that there exist an optimal flow rate which promotes the largest nucleation rates: this is due to the fact that moderate amounts of shear enhance the frequency of collision among particles but it is still not large enough as to destroy by shearing forces the incipient crystalline nucleus.
In addition to the crystallization/aggregation in colloidal systems, we have also worked on the problem of how DNA polymers wrap around histones [50].
We also have studied the adsobtion of neutral polymers on homogeneous [48], and stripped surfaces [49], as well as the force betwen two particles coated with neutral polymer brushes when one gets clossed to the other [53]. For this late case we have studied both the planar case as well as the case of two spherical particles coated by a neutral polymer brush. Another case we have studied is the behaviour of particles coated by a neutral polymer brush inside a spherical cavity [39].
Collaborators
Amit Chakrabarti, Kansas State University
Christopher Sorensen, Kansas State University
New algorithms for long range interactions
Long Range Interactions & the root of the problem
Formally a potential is defined to be short ranged if it decreases with distance r quicker or similar than where d is the dimensionality of the system. Electrostatic, gravitatory and dipolar interactions, present in many physical systems, are examples of long range interactions. When long range interactions are present in a system, the weight of the interactions comming from far particles is non negligible. This is due to the type of decay of the interaction with the distance: despite the particle-particle interaction decreases with the distance, the number of interactions increases in such way that the total contribution of the far particles may have a weight as large as, or even exceding the one due to the interaction of neighbouring particles.
In studing the behaviour of matter, the presence of long range forces may be a critical factor due to the limited power of current computers makes impossible simulate macroscopic bulky systems [33]. Small systems have a large surface vs volume ratio and therefore surface effects may govern the physics of the system. When long-range forces are present, the scenario to mimic bulky systems is even worse because we will then neglect a substantial part of the long-range interaction.
Then, why we don’t wait a little bit until computers become more powerful? Even if Moore´s law was able to hold on indefinitely, we would still need around two centuries to be able to tackle with systems of the size of about one cubic centimeter. Therefore, it is clear that we need to do some sort of approach in order to mimic bulky systems right now.
How to mimic bulky systems in which long range interactions are present
The straight cut-off (sometimes including a shift) of the long-range interactions have been observed to lead to many unphysical artifacts in the simulations of bulky systems. Although no perfect solution has been found, there exist some approaches to tackle with the problem:
- Reaction Field Methods.
- Periodic Boundary Conditions (artificial periodicity): Lattice-Sum Methods
- Hybrids of the previous two approaches, eg. LSREF (Heinz2005).
- MEMD Maxwell Equations Molecular Dynamics
Our Research: Periodic Boundary Conditions
Frequently, periodic boundary conditions are the chosen approach. When periodic boundary conditions are used, an artificial periodicity is introduced in order to emulate the bulky system. The cell system is replicated and the interactions between the particles in the main cell and the particles located in the replica cells is taken into account and added to the interactions between particles of the main cell. For this reason, this kind of methods are also known as Lattice Sum Methods. When one performs this kind of sums by brute force, the method is known as Direct Sum.
Despite it seems very easy to perform a Direct Sum, it is in fact very tricky because this kind of sums have a conditional and very slow convergence, which implies that many terms must be included to obtain a reasonable accuracy for the value of the interactions.
Our research in this topic is intended to improve the efficiency of most important numerical algoritms for computing soft matter systems, as well as provide efficient estimates of the error made when setting the different parameters of these methods so the computational effort is reduced as much as possible [24] [27] [28] [41] [43] [46]. This is very important as far as in many industrial sectors the research done through computer simulations is highly dependent on these kind of numerical methods, and long-range forces constitute a bottleneck. Thus, for instance, faster and optimized methods for simulating drugs and other related soft-matter sytems can help to screen much more molecules in the same amount of time, leading to find the right candidate molecules faster.
Another topic related to this is the study of the hydrodynamic interactions which can also be long-ranged in its nature. In particular, refered to hydrodynamic interactions, we are very interested in the fluid-structure interaction as it occurs in the case of the glycocalyx: see please the section devoted to glycocalyx for further information on this special case.
Collaborators
Dr. Vincent Ballenegger, CNRS, Institut UTINAM, Besancon, France
References
[Heinz2005] Heinz et al , JCP 123, 034107, (2005)
AI methods applied to Soft Matter
Recent advances in AI have supposed a boost in many areas of knowledge, and Soft Matter is a field of research that could largely benefit from it. In particular we have focused in two lines of research to apply AI methods to Soft-Matter:
- The use of AI to improve the detection and prediction of phase transitions [1].
- The use of AI to further accelerate the algorithms dealing with long-range forces. (See specific section devoted to long-range interactions)
Collaborators
Human diseases
In collaboration with professor Francisca Barcelo we have done an experimental study [20] about Monoclonal gammopathy of undetermined significance (MGUS). MGUS is a premalignant proliferative disorder that may progress to multiple myeloma, a malignant plasma cell neoplasia. Estimates predict that over a 3% of population will suffer MGUS: for those people the probability of MGUS to develop into multiple myeloma increases circa a 2% yearly in the most positive cases: 18% proability in 10 years, 33% probability in 20 years, 45% probability in 30 years).
Our aim was to analyze via DSC (differential scanning calorimetry) the plasma of patients at different stages of the disease and compare them with that of a healthy control group of people. We seek for differences in the DSC thermograms that could be used to determinate via DSC-thermograms if a person has MGUS or not. Our results proof that that was the case, and that therefore DSC analysis was a promising methodology for a cheaper and faster replacement of testing methodologies used till then for early diagnoses and monitoring of MGUS.
Collaborators
Dipole Matter at lattices
In collaboration with Dr. Josep Batle we have done a series of studies intended to analyze the behaviour of classical dipole matter when constrained to be in a lattice. We have dealt with aperiodic lattices [3], propagation of the magnetic interaction [8].