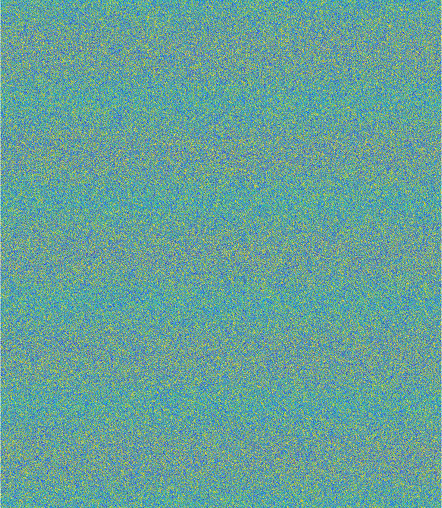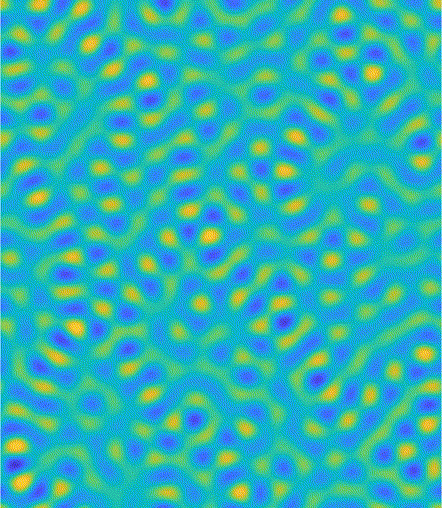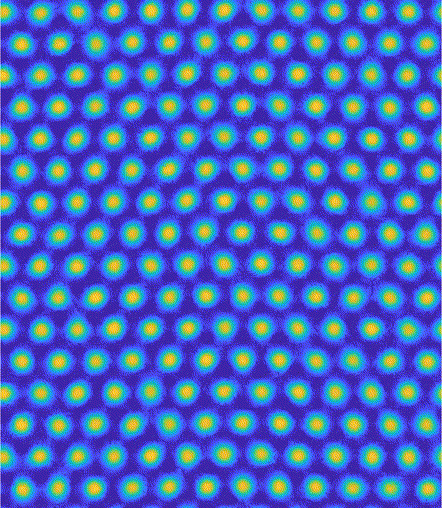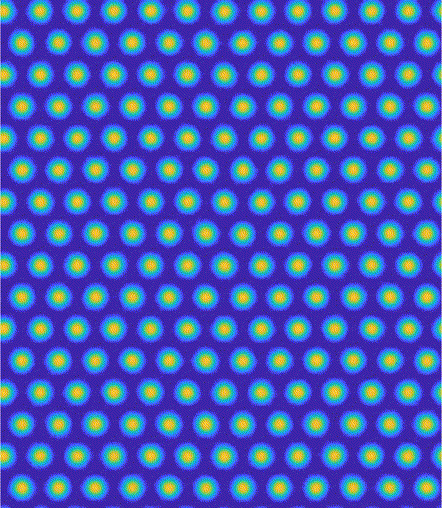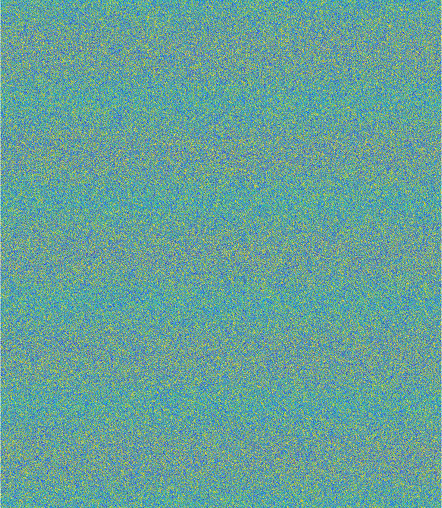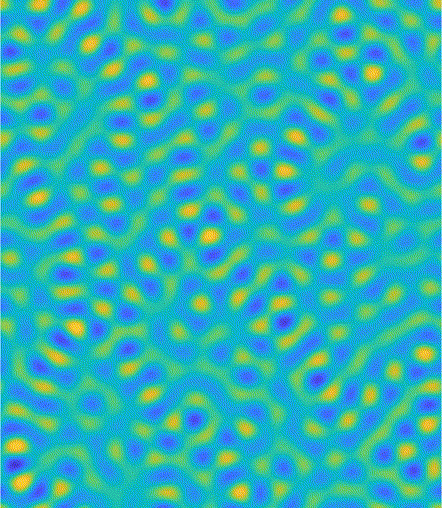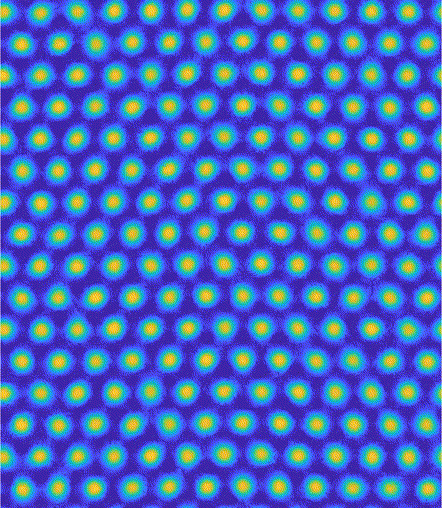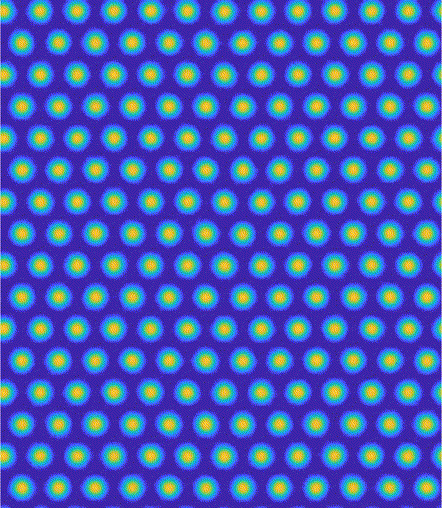Nonlinear Waves
Nonlinearities are crucial for the description of nature.
On a fundamental level, whenever there are interactions between parts of the system if there is a feedback
nonlinearities emerge naturally.
They can lead to intricate and rich physics. This includes phenomena such as excitability, which underlies
cardiac dynamics and the functioning of our brain cells and the emergence of complexity, such as pattern-formation
in ecology, biology and physics. Control and tuning of such nonlinearities is particularly
attainable in optical and light-matter interacting systems which therefore forms a particularly prominent
platform to investigate these phenomena. Our group focuses on extended systems which support waves, from the mean-field limit where many atoms are involved to the onset of
quantum phenomena. In the following we describe different aspects of nonlinear waves and thereby some of our research lines in more detail.
Excitability
Excitability plays a crucial role for cardiac and neurodynamics as well as certain chemical reactions, such as the Belousov-Zhabotinsky reaction,
and represents an extremely nonlinear phenomenon.
In a nutshell, a system is excitable if there is a stable fixed point which -- upon perturbing the system beyond a certain threshold -- can be left and
an excursion in the state space occurs, which later often leads to a return to that fixed point after a long refractory period.
An example for that is the bursting of a neuron or the beating of the heart.
Beyond that, there is a discipline within nonlinear optics that aims at mimicking and exploiting this excentric behaviour.
Our group is involved in an exciting European project that pursues using this behaviour to make lasers on a nanometer-scale.
Bifurcation Theory
As it is often complicated to fully comprehend the dynamics of nonlinear systems in a comprehensive manner.
Similarly to having a street map in a big city, it is often useful to "map out" the steady-state solutions of a dynamical to gain insight into how the system
is organised in order to navigate efficiently or find interesting parameter regions.
Pattern-formation & Complexity
The emergence of global ordering of a dynamical system through the interaction between parts of that system is a rich topic in and of itself, and is commonly referred to with the
umbrella-term complexity. The appearance of patterns in ecological or biological systems is fascinating, and Alan Turing is an early pioneer in mathematically formalising the description of such patterns.
We are interested in the emergence of spatial or spatiotemporal patterns in optical and ultracold atomic systems. In the case ultracold atomic ensembles, such spatial density patterns can excibit
superfluidity, therefore they are called supersolids if that is the case.